Cet article est dédié à Gilbert Deray, qui a affirmé dans un tweet que je ne savais pas lire le rapport cité dans mon article du 21 juin.

Quand j’avais 5 ans, au cours préparatoire, mon institutrice nous enseignait les « mathématiques modernes » sur le sol en linoléum de notre salle de classe en préfabriqué en traçant à la craie des ensembles dans lesquels nous devions placer des objets en fonction de leur forme et de leur couleur. Nous y apprenions alors les notions de réunion et d’intersection : l’ensemble des carrés verts était l’intersection de l’ensemble des carrés et de celui des objets verts, mais l’ensemble des carrés était la réunion des ensembles de carrés rouges, de carrés verts et de carrés bleus (de mémoire, il n’y avait que 3 couleurs ; s’il y en avait aussi des jaunes il fallait évidemment les ajouter).

En dehors de considérations futiles du genre « j’ai envie de sortir en boîte » ou « j’ai envie de prendre l’avion pour les vacances », les questions que chacun devrait se poser pour savoir s’il a intérêt ou non à se faire vacciner contre la COVID-19 sont :

1. Le vaccin est-il sûr ?
2. Le vaccin est-il efficace ?

Pour la question 1, nous avons déjà vu à la lumière des données du VAERS que rien n’est moins certain, particulièrement si l’on prend en compte l’absence de recul temporel sur les effets secondaires.

La question 2 mérite d’être précisée : s’agit-il d’éviter une infection (ou de minimiser la probabilité d’être infecté), même sous ses formes légères, voire absolument impossibles à détecter sans moyens biochimiques (les fameux « cas asymptomatiques »), ou seulement d’éviter les formes graves de cette infection, et surtout bien évidemment, celles conduisant au décès ?

Vu la réponse expérimentale apportée à la question 1, il semble naturel de plutôt mettre l’accent sur les formes graves et les décès, car il paraît bien risqué de vouloir éviter quelques désagréments passagers au prix d’un remède préventif qui pourrait être pire que le mal.

Or, quand on juge de l’utilité d’une vaccination, on se pose implicitement, même si on est allergique aux mathématiques, une question de probabilité conditionnelle : on se demande si l’on a vraiment moins de (mal)chance de tomber gravement malade ou de décéder sachant qu’on est vacciné, par rapport à la même question, sachant qu’on n’est pas vacciné. Et il est souvent utile, pour résoudre ce genre de problème, de se représenter les différents cas possibles sous formes d’ensembles, comportant pour certains des parties communes (des intersections non vides).

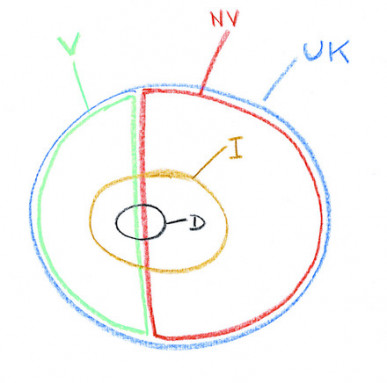
C’est l’objet du petit dessin en début d’article, qui vise à représenter graphiquement une partie des données du tableau 4 issu du document que nous avions déjà utilisé dans un article précédent, et que je reproduis encore ci-dessous :

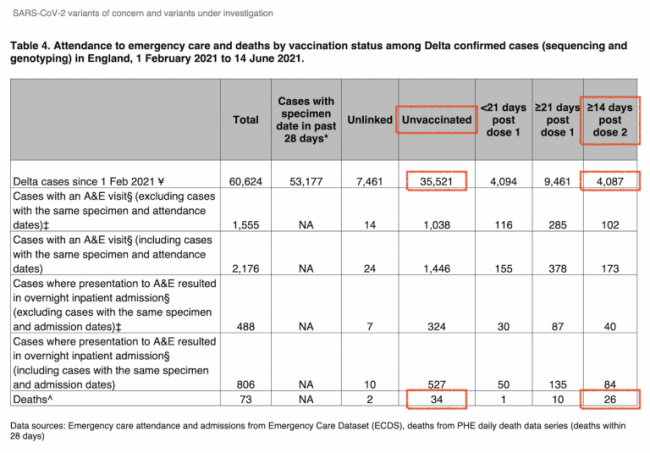
Nous allons nous intéresser uniquement aux données encadrées en rouge, c’est-à-dire aux nombres de cas du variant « delta » et aux nombres de décès pour, respectivement, les personnes non vaccinées et celles qui ont eu leur deuxième et dernière dose depuis plus de 14 jours. Ces chiffres vont nous permettre, d’une part d’estimer l’efficacité du vaccin en conditions réelles, et d’autre part de voir si ce vaccin en vaut la peine pour la diminution de la mortalité.

Dans notre petit dessin à la craie, nous avons tracé un grand ensemble appelé UK qui représente, non la totalité de la population du Royaume-Uni, mais uniquement celle qui est soit pas du tout vaccinée, soit complètement vaccinée contre la Covid-19. Cet ensemble est divisé en deux parties : V désignant l’ensemble des personnes (entièrement) vaccinées, et NV désignant celui des personnes non vaccinées. Le tableau reprenant des données au 14 juin, et pour des personnes totalement vaccinées depuis au moins 14 jours, nous devons rechercher le nombre de personnes totalement vaccinées au 31 mai ; différentes sources nous disent qu’il y avait 37,9 % de la population du Royaume-Uni entièrement vaccinée le 31 mai 2021, ce qui fait, pour un pays de 67,9 millions d’habitants, environ 25,7 millions de personnes. Quant aux personnes non vaccinées, puisqu’au 14 juin les vaccinées (1 et 2 doses) représentaient 61,6 % de la population, les sujets non encore piqués constituaient 38,4 % de la population soit 26,1 millions de personnes environ. Nous avons donc déjà les nombres d’éléments – les mathématiciens diraient les cardinaux – des ensembles V et NV.

À l’intérieur de l’ensemble UK, nous pouvons tracer l’ensemble I des personnes infectées par le variant « delta », qui est à cheval sur les ensembles V et NV puisqu’il y a à la fois des personnes totalement vaccinées (au nombre de 4 087) et des personnes non vaccinées (au nombre de 35 521) qui ont été infectées.

Puis à l’intérieur de l’ensemble des infectés, nous pouvons tracer l’ensemble des personnes décédées, noté D, puisqu’il faut avoir été infecté pour décéder de la Covid-19. Comme l’ensemble I, il est à cheval sur les ensembles V et NV puisqu’il y a eu des morts dans les deux « camps ».

Attention ! La représentation graphique n’est pas du tout « à l’échelle », la taille des différents ensembles n’étant pas du tout représentative du nombre d’éléments qu’ils comportent. Il s’agit seulement de pouvoir visualiser les inclusions (par exemple, D est nécessairement inclus dans I) et les intersections des ensembles (le fait qu’une partie des vaccinés soit décédée, par exemple).

Avec tout ce qui précède, nous pouvons maintenant compléter notre dessin en y inscrivant les cardinaux des différents ensembles, donnés par le tableau ou obtenus par addition de deux nombres (par exemple, le cardinal de l’ensemble D est égal à 34 + 26 = 60) :

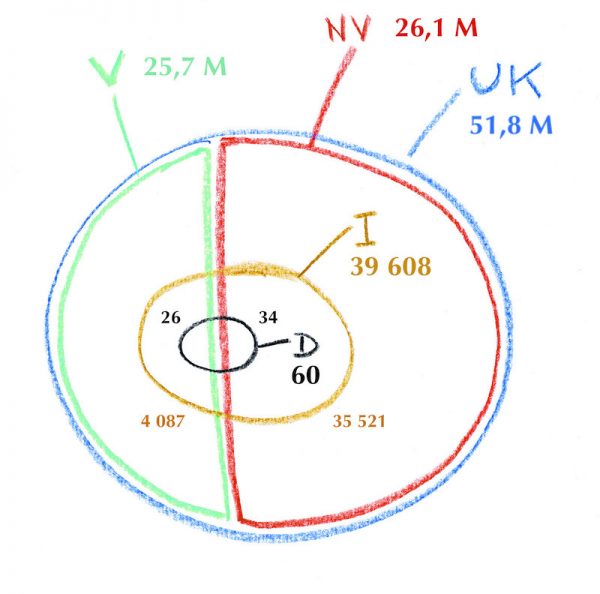
Il devient maintenant plus facile d’estimer les probabilités conditionnelles dont nous parlions. Mais attention, commençons par une mise en garde : lorsqu’on parle de probabilités, on fait comme si les éléments d’un ensemble étaient tous équivalents, et qu’on fait un tirage au hasard parmi ces éléments. Par exemple, on supposera que tous les individus de l’ensemble « vaccinés » sont équivalents, et que tous ceux de l’ensemble « non vaccinés » le sont aussi, et on s’identifiera à l’une ou l’autre de ces catégories pour en déduire telle ou telle probabilité, comme celle d’être infecté ou celle de décéder. Or en matière de santé, c’est un raisonnement grossier, pour ne pas dire faux : énormément de facteurs entrent en jeu, et il n’est pas sûr du tout que la classification « vacciné ou non vacciné », dont on tente de nous faire croire qu’elle est essentielle, soit le déterminant le plus important. Bien d’autres facteurs, certains contre lesquels on ne peut rien (l’âge, le sexe…), d’autres pour lesquels on peut beaucoup (l’alimentation, l’hygiène de vie…) sont sans doute aussi déterminants, voire davantage, pour déterminer la probabilité d’être infecté ou de mourir d’une maladie, que le fait d’être vacciné ou non contre cette maladie.

Il est particulièrement important de garder en tête cette limite au raisonnement : ce n’est pas parce que certains vous disent en permanence à quoi il faut penser que la classification qu’ils vous imposent est réellement importante pour la question posée. Mais puisque c’est ainsi que fonctionnent les évaluations de l’efficacité des vaccins, en mettant dans le même sac des individus que tout oppose et en faisant comme si le vaccin pouvait être le paramètre déterminant qui effaçait tous les autres, soyons aussi bourrins que les chercheurs de l’industrie pharmaceutique et utilisons les chiffres officiels de Public Health England pour en tirer quelques conclusions.

Lire la suite de la démonstration de François Roby sur aitia.fr